※ 메르님의 글을 투자로 확장하기 위해 오렌지보드에서 제공하는 정보입니다. 하워드 막스가 말하는 2차 사고의 개념입니다.
※ 필자와 저자의 의견이 일치하지 않을 확률이 높습니다. 댓글 남겨 주시면, 메르님께서 답변을 주시기로 하셨습니다.
※ 하술한 내용은 투자를 권유하기 위함이 아닙니다.
※ 본 서비스를 통해 발생한 운영자의 수익은 메르님과 협의에 따라 모두 기부합니다 (운영비 제외).

---

<목차>

관련글

구성의 오류

팃포탯(Tit-for-Tat)

   1차 대회

   2차 대회

   Golden Balls

리처드 도킨스가 말하는 진화

룬샷

워렌 버핏

결론

---

관련글

메르님께서 가끔씩 게임이론이나 팃포탯에 대한 글을 쓰십니다.

 

저도 과거에 이것저것 정리해 놓은 글이 있어서 정리하여 포스팅해 봅니다.

 

어떤 마음가짐으로 살아야 하나에 대한 가이던스로 전 회사 동료 대상으로 세미나를 한 적이 있습니다. 반응이 나름 좋았습니다.

 

주) 팃포탯 내용은 주로 나무위키 내용을 참고 하였습니다.

 

 

구성의 오류

 

시장 실패의 경우 중 구성의 오류라고 있음.

부분적으로 성립하는 것이 전체적으로 성립하지 않는 경우를 말함.

 

축구장에서 맨 앞줄의 사람이 더 잘 보려고 일어서면, 그 뒷줄 사람이, 그 뒤뒤줄 사람도 일어나서 보게 되므로 다리만 아프게 되는 경우를 말함.

 

개인 차원에서 합리적 선택이 전체에서 합리적이지 않는 경우를 ‘구성의 오류’라고 함.

구성의 오류 대표적인 사례가 저축의 역설(Paradox of Thrift)과 죄수의 딜레마임.

 

저축의 역설은 영국의 유명한 경제학자 존 메이나드 케인즈가 제기했음.

 

이런 메커니즘임.

1. 잘 살려고 저축에 집중하면, 소비를 줄여야 함.
2. 소비를 줄이면, 물건이 팔리지 않음.
3. 생산품이 팔리지 않아 재고가 쌓임.
4. 더 생산할 필요가 없어 고용을 줄임.
5. 일자리가 줄어듦.
6. 1번에서 5번이 반복되면 불황임.
7. 내 일자리도 위협 받음.

 

여담으로 우리나라 실학에서도 중농주의는 절약을 강조하고, 중상주의는 소비를 강조함. 

뭐든 극단으로 치달으면 좋지 않음.

 

케인즈는 시장의 기능이 실패할 수 있으므로 정부의 개입이 필요하다고 주장함. 그 유명한 유효수요 (Effective demand)이론임.

 

다른 대표적인 사례가 죄수의 딜레마임.

 

용의자A와 용의자B가 서로 다른 방에서 취조를 받게 됨.

 

인센티브와 페널티가 있음.

- 둘다 침묵하면 각각 6개월씩 복역함. 합계 12개월임.

- 둘다 자백하면 둘다 6년씩 복역함. 합계 12년임.

- 한 명이 침묵하고, 한 명이 자백하면, 자백한 사람은 석방, 침묵한 사람은 10년 복역함. 합계 10년임.

죄수A의 선택을 생각해 봄(B의 입장도 마찬가지임).

 - B의 침묵이 예상되면, 자백하는게 유리함. A는 석방됨.

 - B의 자백이 예상되면, 자백하는게 유리함. 침묵하다가 독박쓸 수 있음.

침묵하면 6개월 혹은 10년을 감옥에서 살아야 되고, 자백하면 석방되거나 6년을 살아야 됨.

모두 자백하는게 유리함. 

 

둘을 단절된 공간에 가만히 냅두면 각자가 합리적인 선택을 하게 됨.

각 6년, 합 12년을 살아야 하는 악수를 두게 됨.

개인으로 합리적인 선택이 전체로는 비합리적인 결과를 도출함.

 

죄수의 딜레마는 정보비대칭을 해소하는 역할이 필요함을 설명할 때 사용됨. 중간자가 상황을 알려주면 둘다에게 좋은 선택을 할 수 있게 됨.

 

잘 사용해야 함. 큰 정부의 근거로 사용될 수 있음. 정부의 역할은 구성의 오류를 해결하는 정도로 정하는게 좋다고 생각함.

 

실제 이런 사례를 통계적으로 검증한 것이 아님.

모두 사고 실험임. 투자자가 갖춰야 될 능력임.

팃포탯(Tit-for-Tat)

 

시장 구성원들에게 자유롭게 의사결정을 맡기면, 구성의 오류가 발생할 수 있음.

 

정부가 소극적이고, 정보비대칭을 해소해줄 중간자도 없는 경우, 시장 참여자가 사용할 수 있는 전략 중 하나가 팃포탯임.

 

게임 이론의 반복적인 게임 상황에서 사용할 수 있는 유효한 수단임.

‘동등한 보복’을 의미하는 영어 속담임. ‘맞으면 친다’ 임.

 

기본적인 전략은 1)처음엔 항상 협력함. 2)이후에 상대가 방금 전 했던 판단을 똑같이 따라함.

좀 더 설명하면, 1)먼저 협력하고, 2)배신하면 보복하고, 3)협력하면 바로 용서하고의 반복임.

단순함. 상대가 내 전략을 알고 있어도 상관없음. 

 

로버트 액설로드 라는 정치학 교수가 1980년대에 당시 유행하던 죄수의 딜레마 문제를 고민하고 있었음. 반복적인 죄수의 딜레마 상황에서 어떤 전략을 취하는 것이 가장 성공적인지가 고민이었음.

 

컴퓨터를 활용하여 모의 시뮬레이션 대회를 열기로 함.

 

세계 각지의 수학자, 정치학자, 경제학자, 군사 전문가, 게임 이론 권위자 등에게 자신의 대회에 참여해 줄 것을 요청함.

 

과제는 반복적인 죄수의 딜레마 상황에서 최고의 성과를 올릴 수 있도록 프로그램을 짜서 제출하는 것임. 

 

점수판(payoff matrix)임. 

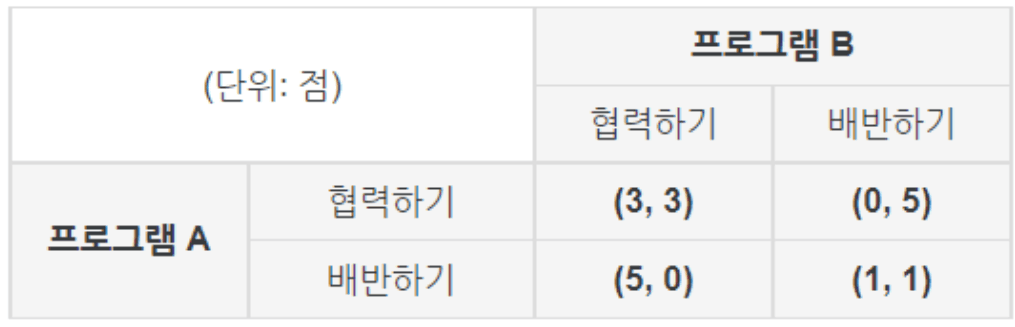
1. A와 B가 모두 협력하면, 3점씩 가짐.
2. A협력하고 B가 배반하면 A는 0점, B는 5점을 가져감.
3. A와 B가 모두 배반하면, 1점씩 가짐.
4. 죄수의 딜레마와 동일한 상황을 게임화함.

 

대강 1분 20초 정도부터 보면 됨. (영어를 몰라도) 규칙을 알 수 있음.

The Iterated Prisoner's Dilemma and The Evolution of Cooperation

 

1차 대회

 

200회 반복시행함 (한 시행을 회차라고 표현).

게임참여자는 과거 회차의 기록을 참고하면서, 당 회차에 임할 수 있음.

참여한 모든 프로그램과 1회의 게임을 치름. 리그전임.

회차가 거듭될수록 누적된 자료/이론/전략을 모두 오픈함.

 

대회 참가 프로그램은 14개임. 심리학, 경제학, 정치학, 수학, 사회학 등의 전문가 집단에서 참여함.

 

우승자는 팃포탯 전략을 사용한 토론토 대학교의 아나톨 라포포트(A.Rapoport) 임. 504.5점을 획득함.

 

아나톨 교수는 우직하게 팃포탯을 고수했고, 다른 13명은 팃포탯을 변형한 전략을 사용하였음. 오리지널에 모두 패함.

 

1차 대회의 교훈#1. 잔머리 굴리지 말고 선하게 굴어라.

• 먼저 배반하지 않는 ‘선량한’ 프로그램들이 상위를 싹쓸이함. 472~504점을 획득함.
• 선제 배반한 ‘교활한’ 프로그램 중 가장 성공한 것이 401점이었음.
• 특히, 선량한 프로그램이 선량한 프로그램을 만나면 완벽한 협력이 나타남.
  (사람도 사람을 잘 만나야 함)
• 교활한 프로그램끼리 만나면 서로 뒤통수치다가 점수를 얻지 못함.
• 5점 따려는데 집중한 전략은 결과가 좋지 않았음.

 

1차 대회의 교훈#2. 대인이 되어라.

• 고득점을 획득한 프로그램은 1)먼저 배반하지 않고 2)협력을 청해오면 관대하게 용서하는 프로그램이었음.
• 철저한 보복을 위주로 취한 전략은 결과가 좋지 않았음.

 

1차 대회의 교훈#3. 상대가 내 패턴을 알게 하라.

• 어떤 프로그램은 자신의 전략을 상대가 알기 어렵게 했음. 상대가 전략을 알 수 없으니 배신하는 결과가 많이 나왔음.
• 팃포탯은 상대에게 자신의 전략을 완전히 노출시켰음에도, 상대를 자신의 룰에 맞게 강제함.
• 상대가 자신의 전략을 알 수 있기에 티키타카가 나온 듯함.

2차 대회

 

1차 대회의 결과가 흥행함. 2차 대회를 공지함.

1차 대회 분석 데이터를 전체 오픈함.

규칙을 바꿈. 1번째 대회때는 200회 한정 시행이라 200회에 배반하는 경우가 많았음.

2차 대회에서는 언제 게임이 끝날지 모르게 바꿨음.

62개의 프로그램이 참가함. 심리/경제/정치/수학/사회학 등 전문가 집단과 일반인이 참가함.

 

이번에도 우승자는 팃포탯을 사용한 토론토 대학의 아나톨 라포포트 였음.

 

2차 대회의 교훈

• 참가자들의 가방끈(학력)은 점수와 무관하였음.
• 더 극명하게 밝혀진 것은, 팃포탯에 수정을 가할수록 승률이 감소했음. 점수 조금더 얻으려고, 살짝 조작하면 오히려 실패했다는 말임.
• 1차 대회의 결과는 용서와 화해를 해야 점수를 잘 딴다는 걸 보여 주었음.
  재미있는 점은, 프로그램의 상당수가 더 잘 화해하는 선량한 프로그램을 만드는게 아니라, ‘선량한 프로그램을 적절히 등쳐 먹자’ 를 목적으로 만들어짐. 상대방의 관대함을 이용해야 겠다는 심보임. 팃포탯은 선공을 하지 않으나, 배반에는 응징했고, 화해의 손길에는 화답해줌.
• 최초 10회 정도의 시행에서 이 조련? 작업이 완료됨. 이후 시행에서는 티포탯과 상호협력하거나, 공멸하거나 둘 중 한가지였음. 팃포탯을 이기고 싶으면 점수를 줘야 했고, 망하게 하려면 나도 망해야 했음. 팃포탯은 지기 어려운 전략이었음.

Golden Balls

 

영국의 방송국이 팃포탯을 tv프로그램으로 만들었음. ‘Golden Balls’ 임 (2007).

 

참가자 두 명이 마주보고 앉아서 서로 설득하다가, 스플릿 혹은 스틸을 선택해야 함.

 

둘다 스플릿을 선택하면, 모인 상금을 절반씩 나눠 가짐.

한 명이 스플릿, 한 명이 스틸을 선택하면 스틸한 사람이 모두 가짐. 

둘다 스틸을 선택하면, 둘다 아무것도 얻지 못함.

이런 식임. 표정이….

동영상을 보면 재미 있음. 여자는 남자에게 자기가 스틸을 선택하면 나는 나쁜 년이 될 것이고, 내 지인들이 나를 엄청나게 욕할 거라면서 울상을 지으며 스플릿을 해달라고 애원함.

 

How To Spot A Liar (£100,000 Split or Steal) (Using Statement Analysis)

 

결과는 영상으로...

다른 사례도 있음.

 

오른쪽 남자는 자기는 무조건 스틸을 선택하겠다고 함. 내가 다 가지던지, 우리는 아무것도 가지지 못하게 될 거라고 말함. 왼편의 남자는 기분이 많이 상함. 대신, 너(왼)가 스플릿을 선택하면 내가 따로 만나서 나눠 줄게 라고 설득함. 결과는? 영상을 확인바람.

golden balls. the weirdest split or steal ever!

팃포탯 콘테스트나 위 방송에서처럼 타인에게 협력을 끌어내는 건 쉽지 않은 일임. 매우 어려움.

 

팃포탯이 가이드라인이 될 수 있음.

주의) 은근슬쩍 와이프한테 해 본적이 있는데, 안통함. 싸움날 수 있음. 어리석게도 대차게 배반할 각오를 해야 한다는 걸 몰랐음. 가족 이외 커뮤니티에 더 적합한 듯.

리처드 도킨스가 말하는 진화

작은 돌연변이가 성공적인 진화를 만든다.

 

신, 만들어진 위험(2021) (by 리처드 도킨스)이라는 책에 나오는 내용임. 

 

우리가 치타의 딱 한 부위만을 무작위로 바꾼다고 가정해 봄. 

핵심은 아주 조금만 바꾸는 것임. 

 

가령 치타가 이전 세대보다 조금 더 긴 발톱을 가지고 태어난다고 가정해 봄. 

아주 조금만 바뀌었을 뿐이지만, 이 작은 변화 때문에 이제 치타는 생존에 약간 더 불리해졌거나, 유리해졌을 가능성이 높음.

살짝 긴 발톱은 땅을 더 안정감 있게 디딜 수 있게 해주고, 조금더 빨리 달리는데 도움을 줄 수 있음. 가젤을 잡을 때, 순간 도약이 향상되거나, 더 잘 움켜쥘 수도 있음.

달리기 선수 런닝화에 박힌 스파이크 같은 역할이 커질 수 있음.

 

이 때 중요한 것은 작은 변화임. 작은 변화일 수록 더 나은 변화일 확률이 큼.

 

변화가 매우 크다고 가정하면 왜 작은 변화가 좋은지 이유를 자연스레 알게 됨.

발톱이 1피트(30센티미터)로 변했다면, 생존에 위협이 됨. 잘 달리지도, 잘 움켜쥐지도 못할 확률이 높음.

 

자연에서 변화는 돌연변이임.

어느 방향으로든 큰 돌연변이는 해로움. 

반면, 작은 돌연변이는 유익할 확률이 더 높음.

 

다윈은 성공적인 돌연변이는 거의 항상 작은 것임을 깨달았음.

작은 돌연변이는 포착하기가 어려워, 과학자들이 연구하는 돌연변이는 보통 큰 것임.

일부 사람들이 모든 돌연변이가 생존에 불리하다고 생각하게 된 배경임.

다윈은 가축, 작물의 사례를 들며 사람들에게 자연선택의 힘을 납득시킴.

 

종의 기원의 첫 말은 ‘자연은 도약하지 않는다’ 임.

 

인간은 야생마의 품종을 수십 가지로 바꾸었음.

짐마차용 말과 중세 군마 같은 종은 야생마보다 훨씬 큼.

우리 조상들은 매 세대 가장 큰 개체를 선택해 번식시킴으로써 짐마차용 말을 만들었음.

 

다윈의 위대한 점은 자연에서는 인간 선택자가 필요없다는 사실을 깨달았다는 데 있음. 

자연은 모든 일을 수억 년동안 해 왔음.

어떤 돌연변이는 생존과 번식에 유리하고, 그런 유전자는 개체의 수가 많아짐. 반대의 경우도 작용함.

 

성공적인 돌연변이는 무작위적이며 변화가 작다는게 핵심임.

무작위적으로 발생하지만 엉망진창은 아님.

 

각각의 무작위적인 변화가 그 동물을 앞 세대와 아주 조금만 달라지게 만들었고, 지금까지 이어져 온 것임.

결론) 작고 꾸준한 변화가 위대하면서 동시에 부작용이 적음. 

룬샷

 

아래 내용은 ‘룬샷’ 이란 책에 나오는 내용임. 

구조나 환경에 대한 내용임.

 

스타트업 사업가들은 대기업이 자주 실패하는 이유가 대기업형 사람들이 보수적이며 리스크 회피적이기 때문이라고 말함.

 

본인들은 리스크를 기꺼이 감수할 진정한 열정을 가졌다고 자부하고,

그렇기 때문에 작은 기업에서 흥미진진한 아이디어가 나오는 것이라 믿음.

 

그런 고식한 대기업형 사람을 스타트업에 넣었다고 가정해 봄.

오히려 그는 과격한 아이디어를 옹호하려고 테이블을 쾅쾅 내려칠 것임.

똑같은 사람이 어떤 맥락에서는 보수주의가 되고, 다른 맥락에서는 혁신주의자가 됨.

 

사람 탓이 아님.

구조 혹은 포지션이 그런 선택을 하게 만드는 거임.

 

물 표면을 망치로 내리치면, 물이 튀고 망치는 가라 앉음.

물을 얼린 다음 내리치면? 표면이 부서지거나 망치가 부러짐.

같은 분자가 환경/구조에 따라 액체가 되기도 하고, 고체가 되기도 함.

 

물 분자 하나를 떼어내서, 얼음 덩어리 위에 떨어뜨리면 얼음이 됨.

수영장에 떨어뜨리면 다른 물 분자에 섞여 버림.

 

물 분자가 변한 것이 아님. 구조가 변한 것임.

온도가 내려가면 결합 에너지가 강해지고, 무질서(엔트로피)가 약해짐. 

두 가지 힘이 역전될 때 시스템의 전환이 일어남. 

이를 '상전이'라고 함. 구조가 물분자의 행동을 결정한 것임.

 

의견) 저자는 문화가 아니라 구조의 작은 변화를 통해 조직을 바꿀 수 있다고 얘기하고 있음. 위에서 말한 버나드 부시의 과학연구개발국 과 같은 활동이 룬샷을 키우는 활동임.

워렌 버핏

 

버핏 한 말들은 대부분 인상적임.

많이 봐서 그런가, 말만하면 명언인 것 같은 착각이 들 정도임.

이번엔 자신을 돌보는 것이 중요하다는 내용을 가져와 봄.

2002년 주주총회에서 문답한 내용임.

 

"워런이 은퇴에 대해서 뭘 안다고..." (버핏 & 멍거)
https://www.youtube.com/watch?v=TM8yzv-fdZY 

 

한 남자가 은퇴 후 고등학교에서 학생들을 가르치고 있다고 함. 투자 과목임.

학생들에게 은퇴를 어떻게 대비해야 할지 가르쳐 달라고 함.

 

나머지는 영상에서…(길지 않아서 다 보시는 걸 권유합니다.)

결론

 

위의 각 섹션에서 나온 내용의 핵심을 요약해 보았습니다. 스토리 텔링을 어떻게 하냐에 따라 비슷하고 당연한 말들이 다르게 느껴지는 경우가 많습니다.

 

1. 협력하라 (다른 사람과 잘 지내라).
2. 교활하게 머리 굴리지 말고, 선량하게 굴어라.
3. 대인이 되어라 (관대하되 단호하라).
4. 자신의 의사결정 패턴을 상대방이 알게 하라 (복잡하게 굴지 마라).
5. 조금씩 업그레이드 하라.
6. 구조에서 원인을 찾아라.
7. 자신을 소중히 하라.

꽤 유용한 삶의 지침입니다. 더 나은 사람이 되기 위해서일 뿐 아니라, 나의 이익을 높이는 방향이기도 합니다.

 

감사합니다. 

 

메르xOB 드림